Speculative Bubble
Produced by Giacomo Bellavita
1. DEFINITION OF BUBBLE
As said in the introduction, bubbles are generally defined as periods where financial assets are traded in high volume, at prices significantly higher than the fundamental value (Shiller, 2006).
Can we detect such mispricing effect? The short answer is yes, there are some econometric tests that can be used to detect for asset price bubbles. However, this answer comes with two major warnings. First, this doesn’t imply that we can predict when a bubble will burst, and secondly, econometric models works beautifully until they don’t. Before delving deeper in reviewing some, among the numerous methods to detect bubbles, it is useful to take a bird view and explore some key features of financial bubbles as described in the scientific literature. This will allow us to grasp some general understanding of the mechanics behind financial bubbles that will be useful later when considering the various methods available in the literature to test for bubbles.
Although several specifications of asset price bubbles have been put forward in the literature, a formal, widely accepted definition of asset price bubble is the one pioneered by Blanchard (1979). After his research, a large and growing number of papers used his specification of rational bubbles to describe asset price misalignment. Blanchard and Watson (1982) further enhance the introductory work of Blanchard (1979), pointing out that under the assumption of rational expectation, asset prices do not have to reflect solely their fundamental value. In other words, there can be rational deviations of the price from its fundamentals, i.e. rational bubbles1.
To show this, let us consider the single period identity that links asset prices, future cashflows, and returns. For an asset that has a constant positive expected return, R , its price, P , is a linear function of future expected cashflows. Considering the case of a stock, whereby denotes the real (ex-dividend) price today (i.e. at the end of period t), is the real dividend that is paid to the owner of the stock between t and t+1 , and indicates the positive rate of return from owning such asset between t and t+1, we have:
Under the assumption of rational expectations, risk neutrality, and further assuming a constant expected return, , the price of a dividend paying stock in a two-period setting equals the present value of all its expected cashflows, namely dividends paid by the stock and its resale value. Algebraically:
Eq. (1.1) is the starting point of most empirical asset pricing tests. However, the literature proposes many different alternatives to Eq. (1.1). As an example, since dividends may not always capture the fundamental value attached to a stock, Diba and Grossman (1988), as well as Phillips et al. (2015), enriched Eq. (1.1) with the process {Ut}, representing the unobservable fundamental component2. Other specifications of (1.1) involve lessening the assumptions made above, for instance the one regarding the constant expected rate of return. Nonetheless, as argued by Phillips et al. (2011), changes to Eq. (1.1) would not change the behaviour and the properties of the bubble but will complicate the analysis of the rational bubble solution. Therefore, without loss of generality, I will disregard the amendments proposed in the literature, at least in this section, and proceed with the standard set of assumptions outlined above. It is worth noticing that Eq. (1.1) is a first-order stochastic difference equation. This implies that the overall set of solutions can be found by solving it forward. By repeatedly substituting subsequent prices, and by using the law of iterated expectations to eliminate future dated expectation, the following result holds3:
And by denoting:
Eq. (1.2) can be written in a more compact way:
Eq. (1.2) represents the entire class of solutions to Eq. (1.1) and reveals that the price of a stock at time t breaks down in two components: the fundamental component (), represented by the discounted sum of the stream of expected dividends, plus a bubble component (), represented by the expected resale value. Under this setup, is called rational bubble, as it is consistent with rational expectation theory. Incidentally, Eq. (1.2) emphasizes that rational bubbles can arise whenever investors include in their information set the expectation of stock’s future price. It is worth highlighting that under this setup, a speculative bubble is not a mispricing effect but a basic component of asset prices. Remarkably, this implies that the price of the asset may exceed its fundamental value if agents expects that they can sell the asset at an even higher price at a future date. To put it in another way, rational bubbles do not imply any irrationality and most importantly, there are no arbitrage opportunities as rational investors are compensated for holding the bubbly asset.
More specifically, in equilibrium, Eq. (1.3) shows that the minimum compensation that an investor receives by holding a rational bubble is the risk-free rate. As argued by Gilles and LeRoy (1992) this condition ensures that there are no risk-free arbitrage opportunities in the marketplace, otherwise, whenever the bubble component does not grow at least at the rate of interest, investors could earn an abnormal profit by selling short the asset spot, invests the proceeds at the risk-free rate and buy the security forward. Moreover, under the assumption of a positive risk-free rate made above it is clear that , therefore, is a stochastic process that satisfies the submartingale property.
Under this setup, within an infinitely lived rational expectation model, the market fundamentals model is a special case of a more general model that allows for bubbles. The no bubbles special case is justified by a transversality condition in infinite horizon models.
More specifically, the transversality condition asserts that the second term in the equation (1.2) is zero. The bubbleless model outlined in many finance textbooks is justified only if two conditions hold contemporaneously. First, note that the market fundamental solution exists only if the constant rate of return is strictly greater than the growth rate of dividends, as in this case, the discounted dividend stream will converge to a positive, nonzero value. Additionally, to have =0 we must impose:
Tirole (1982), makes a formal arbitrage argument that justifies the transversality condition within a rational, infinitely lived model having a finite number of agents. More specifically, if prices are well above market fundamentals, the only reason to hold such an asset would be to sell it at some time in the future and realise the expected capital gain. Within an infinitely lived economy, since investors live forever, there is no incentive to realise the expected capital gain in finite time. Instead, agents would perceive the asset to be overvalued, and would derive additional utility by selling short the bubbly asset forever. This occurs since the loss of utility in doing so (measured by the discounted stream of dividends) is lower than the sale value (fundamental value plus positive bubble). This cannot be the equilibrium since all agents in the marketplace would want to sell the asset whenever they perceive that there is a bubble. Therefore, on a theoretical basis, in a rational, infinitely lived framework bubbles can be effectively ruled out.
However, notwithstanding the soundness of the arguments made by Tirole, the starting point of almost all empirical tests presented in the next section rely on partial equilibrium models of the type outlined above.
2. TESTING FOR BUBBLES
Having clarified what a rational bubble is, this section reports some econometric testing procedures aimed at detecting rational bubbles. Since the literature on empirical tests concerning rational bubbles is in constant evolution, I will first present some older testing procedures that will be useful to enrich the understanding of rational bubbles. After having presented some critiques moved to those testing procedures, I will justify the hunt for better
and more powerful models. More specifically, I will outline the most recent technique to test for the presence of stock price misalignments within a rational bubble framework, namely the Phillips et al. (2015) GSADF algorithm.
UNIT ROOT AND COINTEGRATION BASED TESTS
There have been numerous attempts in the literature to empirically detect rational bubbles, all of them relying on different econometric testing procedures involving different types of time series approaches. However, different techniques, produce diametrically opposing results. A common theoretical starting point for most empirical test is represented by Eq. (1.2) and Eq. (1.3). However, Eq. (1.3) forces the bubble component to grow at the risk-free rate forever. This framework is not sustainable as it would lead the observed price of the asset to diverge towards infinity in finite time. Blanchard and Watson (1982) were the first researchers to put forward a stochastic process describing bubble’s behaviour, compliant with the submartingale property in Eq. (1.3). They modelled 𝐵𝑡 in the most intuitive way: it can take the path of a rapid increase followed by a burst or at least, a sharp decline. The following system of equation clarifies the concept:
Following Blanchard (1979) . In this simple model, will grow with probability 𝜋 for a finite period with explosive expectations while, when state two materialises, it will crash resoundingly with probability 1−𝜋. Interestingly, under this setup, the probability of a crash affects the path of the bubble component. Namely, if 𝜋 decreases and 1−𝜋 increases, the higher the probability of a crash leads to an acceleration while the bubble lasts. Note that while in Eq. (1.3) the investor was compensated with a gross return equal to (1+𝑟), in this setting the bubble is expected to yield a higher return than (1+𝑟), namely >(1+𝑟) to compensate the agent for the positive probability of a burst. Note also that if 𝜋=1 the model collapses to the deterministic bubble described in Eq. (1.3). Lastly, Eq. (2.1) forces the initial value of the bubble, 𝐵0, to be strictly positive. Otherwise, if is assumed to be negative, the value of the bubble grows as time goes by, possibly dragging the price of the asset into negative territory in finite time. Moreover, the case =0 is ruled out by the model itself. More precisely, Eq. (2.1) does not allow the bubble to selfgenerate, therefore, if =0, the expected value of , with 𝑘=[1;∞) would be zero as well. These two last examples make clear why must be strictly positive. In other words, if a bubble materialises it must be always have existed from the first day of trading.
Diba and Grossman (1988) were the first researchers that exploited the theoretical properties of rational bubbles for their detection. More specifically, relying on the theoretical framework of Blanchard (1979), and Blanchard and Watson (1982), they observed that rational bubbles have some unique econometric properties that can be exploited for their detection. For instance, under the theoretical framework presented so far, rational bubbles cannot start “out of the blue”. As already pointed out, in equilibrium, the only way to have a rational bubble in stock prices is considering an initial non-zero positive value of the bubble component, i.e. >0. Additionally, Eq. (1.3) suggests that a rational bubble process is always explosive in expectations and therefore, nonstationary.
Under these assumptions, it is straightforward to conclude that in a bubble-less model (i.e. =0), the degree of non-stationarity of stock prices is entirely control by dividends. More precisely, if dividends are stationary after nth differences, stock prices will be stationary in nth differences. Since in the presence of a bubble this claim does not hold, Diba and Grossman (1988) suggested to use unit root tests to detect the degree of non-stationarity of stock prices and dividends. By applying a Dickey-Fuller tests to the annual real S&P500 series and its real dividends from 1871 to 1980, they found both prices and dividends to be integrated in levels but stationary in differences, vindicating the absence of a bubble in US equity prices.
However, they did not stop here. After having found that stock prices and dividends are both I(1), they noted that whenever =0, stock prices and dividends are related by the dividend discount model equation, hence they must be cointegrated. Otherwise, if this is not the case, deviation from the long run equilibrium would never be corrected, making the very model useless. Therefore, empirical evidence of cointegration between the two series can be taken as evidence against the presence of a rational bubble. Diba and Grossman (1988), applied cointegration tests to the annual real S&P500 prices and real dividends from 1871 to 1980. Again, the results of Diba and Grossman (1988) point towards the absence of rational bubbles in the data as they found prices and dividends to be cointegrated.
Evans (1991) disagrees. More specifically, he argues that standard unit root and cointegration tests do not account for the possibility of periodically collapsing bubbles. Financial history seems to emphasize that bubbles are recurring phenomena that suddenly pops and restart. Therefore, the presumption by Diba and Grossman (1988) that a bubble cannot pop and restart seems not to match the ‘true’ empirical process that drives asset prices in financial markets. Evans (1991), put forward a model that allow the bubble component to collapse to a small, non-zero value, and then continue increasing still following the submartingale property of Eq. (1.3). His model takes the following algebraic form:
Where 𝜓=(1+𝑟), 𝑘 and 𝜏 are positive real constants to be chosen s.t. 0<𝑘<(1+𝑟)𝜏, and is an exogenous process of i.i.d. random variables4. Instead, constitutes an exogenous i.i.d. Bernoulli process, independent of {}, with 𝒫(=1) = 𝜋 and 𝒫(=0) = (1−𝜋) for 0 < 𝜋 ≤ 1. Whenever {=1}, the bubble will continue to grow, whereas the bubble bursts whenever {=0}. Evans’ bubble features two different rates of growth: for 𝐵𝑡≤𝜏, the bubble grows at the mean rate (1+𝑟), while if >𝜏, the bubble ‘erupts’ and grows at the faster mean rate (1+𝑟)>(1+𝑟), but collapses with probability (1 – 𝜋) per period. When the bubble bursts, it falls to a positive negligible value, 𝑘, so that the process is allowed to start again. Evans implemented Monte Carlo simulation of the Diba and Grossman (1988) bubble detection tests, using his own specification for the bubble process, i.e. periodically collapsing bubble. He found that when the bubble component is allowed to periodically collapse, unit roots and cointegration tests perform much worse, failing to reject the no-bubble hypothesis more often than not. The tests pioneered by Diba and Grossman (1988) have difficulty in detecting periodically collapsing bubbles because the latter behaves more like stationary process in finite samples. It is important to note that Evans (1991) does not show the existence of bubbles in stock prices, he only shows that standard cointegration and unit roots tests are not adequate to reject this hypothesis.
THE GSADF TEST
Evans’ critique led to several papers trying to overcome the difficulty of detecting periodically collapsing bubbles. Partly because of the increasing computational power of computers and partly because of the greater availability of data, real time bubble detection monitoring has been made feasible. As a matter of fact, a novel testing approach pioneered by Phillips at al. (2015) has been put forward to detect episodes of periodically collapsing bubbles in financial time series. In a nutshell, this new methodology involves the implementation of a recursive right-tailed variant of the augmented Dickey-Fuller (henceforth ADF) test that is robust to the detection of mildly explosive processes5. More specifically, in the scientific literature, the test pioneered in Phillips et al. (2015) is commonly referred to as the generalised supremum augmented Dickey-Fuller test (henceforth GSADF). The reason that makes such a test particularly robust in detecting bubbles of the rational type is because mildly explosive processes represent a small departure from a unit root behaviour while being consistent with the submartingale property that defines rational bubbles. Moreover, the GSADF test, being based on a recursive implementation of an ADF-like equation, successfully overcomes the critique put forward by Evans (1991) as it successfully detects the non-linearity and structural breaks intrinsic of bubbles phenomena.
Right-tailed variants of the ADF test are informative about mildly explosive or submartingale behaviour in the data and represents a useful warning alert when it comes to rational bubbles detection. As in the classical ADF test, the null is of a unit root process however, being a right-tailed variation of the standards ADF test, the alternative is of a mildly explosive autoregressive coefficient. Formally, the GSADF test is based on the following hypothesis:
As in all testing procedures, also in this case the model specification under the null is important. Being a right-tailed variant of the classic Dickey Fuller test, the starting point of the GSADF test consist by specifying the following random walk process with weak (local zero) intercept:
Where is the generic time series tested for explosiveness, 𝑑 is a constant, T is the sample size, and 𝜂 is a positive coefficient the controls the size of the intercept and drift as T approaches infinity, and is the error . Usually, the model in Eq. (2.3) is completed by adding additional transient dynamics so to conduct more accurate test for exuberance, just as in a standard ADF test.
Again, 𝑦𝑡 is the generic time series under consideration, 𝜇 is an intercept term, p is the maximum number of lags, for i = [1, . . ., p] are the coefficients of the lagged first difference, is the usual error term, and 𝛿 is the coefficient under test.
Before proceeding with describing more formally the GSADF test, some notation is needed. As mentioned before, the GSADF test is conducted by running ADF-like regressions on subsamples of data in a recursive fashion. Let us denote with T the original sample size and let us assume that the original sample is normalised within [0,1]. Let and be fractions of the original sample that define the first and the last observation of a specific subsample. In forward recursive regressions, model (2.4) is estimated repeatedly, over different subsamples [; ] of the original sample of data. More specifically, for each regression, a fraction of the total number of observations, defined as =−, is used to estimate the ADF statistics. Lastly, a pivotal role in the test is represented by , i.e. the fixed initial window size set by the user. More precisely, is the fractional window width of the initial subsample used to initialize the computation of the test statistic. In each subsample, Eq. (2.4) takes the following algebraic form:
Let us denote by and by the coefficient and its corresponding ADF statistics over the subsample [; ] estimated by Eq. (2.5). By letting to range between [;1] and between [0;], the GSADF test is implemented by using subsamples of forward expanding windows. By letting both and to vary, will vary according to the following equation . Note that as progressively moves away from zero, the window size, , shrinks, as the upper bound for 𝑟2 is limited to one. Figure 1 summarises the concepts explained so far, highlighting the nature of the recursive subsamples used to compute the test statistics.
By continuously running ADF type regressions, each estimation will yield to an ADF statistic, leading to a sequence of statistics. More precisely, the number of observations in each regression is [] and the ADF statistics are computed as follows7:
In order to assess whether a time series displays a mildly explosive behaviour or not, Phillips et al. (2015) suggest comparing the supremum value of the sequence with the corresponding right-tailed critical values. Following the notation in Phillips et al. (2015), the supremum value of the sequence can be defined as the GSADF() test statistic:
Under the null of a random walk process with negligible drift, as the model presented in Eq. (2.3), and further assuming 𝑑=1 and 𝜂>0.5, Phillips et al. (2015) derive the asymptotic distribution of the GSADF test statistic given by
Where W(.) denotes the standard Winer process and 𝑑→ denotes the convergence in distribution. For the sake of comparison, the limit distribution of the standard ADF statistic resembles the equation above with the only difference that is set to zero, and ==1.
Given that the distribution of the test statistic under the null is non-standard, the GSADF() test statistic is then compared with the corresponding right-tailed finite sample critical value generated from several Monte Carlo simulations. Whenever the GSADF() exceed the corresponding critical value, the unit root hypothesis is rejected in favour of mildly explosive behaviour.
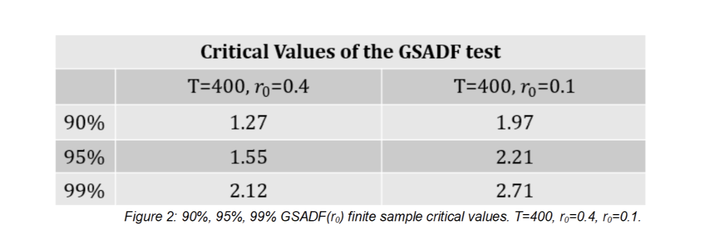
Before going forward with the discussion there is one additional note worth stressing concerning the finite sample distribution of the test statistic. More specifically, the finite sample distribution of the GSADF() depends on . Therefore, changing the initial specification of carries consequence on the estimated critical values. Intuitively, a small value would imply a higher number of ADF-like regression to be estimated, being pickier when it comes to detect mildly explosive behaviour in the time series. To reflect this, critical values would be higher, in absolute value. The opposite happens whenever is set to be large with respect to the sample size9. Wishing to be more practical on this matter, the figure below, offers a re-elaboration of a more comprehensive table reported in Phillips et al. (2015). More specifically, figure 2 illustrates the 90%, 95%, and 99% finite sample critical values for the GSADF statistics. The finite sample critical values are obtained from 5.000 Monte Carlo replications, in which the parameters (𝑑 and 𝜂) under the null has been set to unity while the lag length to zero. The original sample T comprises of 400 observations and critical values have been computed under two different specifications for (i.e. =0.4, and =0.1). As highlighted above, a lower value for 𝑟0 would command higher critical values.
For empirical applications, Phillips et al. (2015) suggest setting in the following way:
Intuitively, if the sample size is big, should be kept small so that the test does not miss any opportunity to detect explosive episodes. On the other hand, if the sample size is small, should be set in such a way to guarantee there are enough observations for an adequate initial estimation.
DATE STAMPING RATIONAL BUBBLES
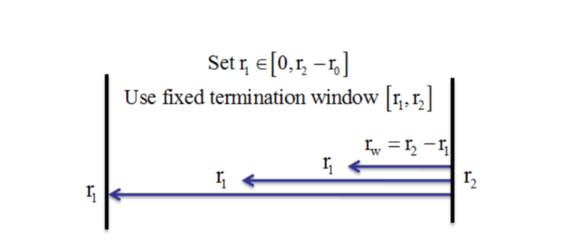
Whenever the null of a unit root is rejected, the inception and termination date of a specific bubble phenomena can be estimated. In other words, Phillips et al. (2015) proposed a method that can consistently date stamp the occurrence of rational bubbles. More precisely, to improve the identification accuracy, the date stamping procedure is based on backward moving subsamples, hence the name backward supremum ADF test statistic (henceforth BSADF). This date stamping procedure is intimately related with the GSADF test introduced before. Interestingly, at the end of this section I will show the nexus between the date stamping procedure and the GSADF test. However, it must be clear that while the GSADF test is aimed at finding enough empirical evidence to reject the null of a unit root, therefore it compares one and only one supremum ADF statistic with one and only one critical value, the BSADF instead compares a time series of supremum ADF statistics with a time series of critical values and whenever the test statistic sequence crosses from below (above) the critical value sequence, the inception (termination) date of a rational bubble can be estimated. More specifically, the BSADF test performs a supremum ADF test on a backward expanding sample of data where in each subsample is kept fix while varies within [0;−]. The following figure clarifies the concept.
Figure 3 is a snapshot of a single subsample taken within the whole sample [0;1]. For each , we derive a sequence of backward ADF test statistics, with ∈[0; - ], and one backward supremum ADF test statistic defined as the supremum value of such sequence, algebraically:
By incrementing one observation at each pass, such that ∈[ ;1], we will end up by having a time series of with ∈[r_0;1]. The estimated origination date of a bubble, denoted by corresponds to the first that exceeds the corresponding simulated right-tailed critical value. Instead, the termination date of a bubble, denoted by , is calculated as the first observation after whose backward sup ADF statistic falls below the simulated critical value sequence. Under this framework we are assuming that the duration of the bubble will exceed , where is a frequency parameter and T denoted the sample size10. More formally, the estimated origination () and termination ( ) dates in fractional terms are calculated as follow:
Where is the backward supremum ADF test statistic given , and is its corresponding right tail critical value, and is the significance level. More specifically, under the null hypothesis of no bubble episodes in the data, the has the following asymptotic distribution:
Where W(.) denotes the standard Wiener process and denotes the convergence in distribution. Therefore, the critical values are defined as the quantile of the above distribution.
As a last note, it is useful to highlight that the GSADF and the BSADF are not different types of tests. An alternative illustration of the GSADF testing procedure in figure 3 is given in figure 4.
More specifically, figure 4 is suggesting that the GSADF test implements the BSADF test repeatedly for each ∈[ ;1], making inferences based on the sup value of the BSADF test statistic sequence.
TESTING FOR SPECULATIVE BUBBLES USING SPOT AND FORWARD PRICES
Although there seems to be consensus in the academic literature about the possible presence of speculative bubbles in crypto, it is useful to formulate models that allow for bubble detection that considers the murky fundamental value of cryptos.
A common feature of all the previous applications of the GSADF test on the crypto space is their reliance on an estimate of a fundamental value, reason being the fact that most bubble tests (including the GSADF test) rely on a composite hypothesis of no bubble and a model for market fundamentals. However, rejecting the null of ‘No Bubble’ may be due to the presence of bubbles or because of model misspecification. Given the opaque nature of cryptos’ fundamental value, we need a test that eliminate the issue of estimating the fundamental value. As we will show below, information on derivatives market can be very useful in this direction.
In this section, I will propose an application of the GSADF test that has been pioneer in ‘Testing for Speculative Bubbles Using Spot and Forward Prices’ by Pavlidis at al. (2017). To the best of my knowledge, this method has never been applied to the crypto space. The advantage of this procedure is that is doesn’t rely on any assumption about market fundamentals, thus, it alleviates any misspecification errors concerning the assumptions of the fundamental component.
The underlying idea is the following: when a bubble is occurring, both the forward exchange rate and the future spot rate will incorporate it but with different weights. This is because rational agents, when forming expectations, correctly attached a non-zero probability for the bubble to burst sometime in the future. Consequently, the forward price becomes a downward bias predictor of the future spot rate, with the difference of the two rates depending on the size of the bubble, and as such, being explosive. To detect such explosiveness in the series resulting from the difference of the future spot and forward rate, I will use a well know test that detects and date stamp mildly explosive processes, the GSADF test (see Phillips et al. 2015). If the risk premium and market fundamentals are non-explosive (a common assumption in the literature), the presence of explosive dynamics in the difference between the two exchange rates can be attributed to the existence of a bubble.
Within the foreign exchange market, under a rational expectation framework, we can rewrite the equation seen in the first chapter. More specifically, the relationship between the log exchange rate , the economic fundamental and the bubble component can be expressed as (Sarno and Taylor, 2002; Engel and West, 2005, chapter 2):
As it will be explained in more detail below, a precise definition of economic fundamentals is not required. Therefore, we will assume for simplicity that follows an autoregressive (AR) process of order one:
As mentioned in the previous chapter, the bubble term follows an explosive AR (1) process, therefore, whenever there is a bubble, the spot rate also has an explosive root.
Under risk neutrality, the log of the forward rate at time t , for delivery time t + n, is defined as:
We can rearrange the previous equation with the help of Eq. (2.10) and Eq. (1.3):
And by rewriting Eq. (2.9) the future spot rate at t + n is given by:
Combining Eq. (2.11) with Eq. (2.12) and netting out expectations, the following result apply:
Where the term consists of two moving average processes, and . By comparing Eq. (2.12) with Eq. (2.14), it is clear that the actual future spot rate is in expectations greater than the forward rate. As noted before, such a difference result from the expectations of the bubble to burst in a future period with probability (following Blanchard’s definition of rational bubbles, Eq. (2.1)). Consequently, the expected growth rate of the bubble , is lower than the actual rate of growth . This is because investors are compensated more and more as the probability of a crash () increases (and decreases).
By subtracting Eq. (2.14) from Eq. (2.12), the following result holds:
As can be inferred from the previous equation, the difference between the spot and the future doesn’t depend on , therefore eliminating the issue of most bubble tests that crucially hinges upon a definition of market fundamentals. However, a major issue of this method relies on the applicability to cryptos, reason being the fact that future prices are not available for every pair of currency, and if they are, there might be some liquidity issue resulting in high bid ask spreads, therefore an analysis with mid prices would not result significant.
Notes
[1] In economics, the rational expectations theory implies that all investors not only understand the structure of the economic model but also use information in an efficient manner as they do not make systematic mistakes when formulating expectations.
[2] The unobservable fundamental component is assumed to be stationary.
[3] This procedure consists of replacing with in Eq. (1.1), then and so on. By exploiting the Law of Iterated Expectations, i.e. , it is possible to derive Eq. (1.2).
[4] More details about are given in Evans (1991).
[5] For a thorough description of mildly explosive process see Phillips and Magdalinos (2007a).
[6] In practical applications, Phillips et al. (2015) set and to unity, while in previous tests, Phillips et al. (2011) set (i.e. random walk without drift). The estimation of the localising coefficient () is discussed in Phillips et al. (2013a).
[7] T denotes the sample size, and ⌊.⌋ is the floor function.
[8] Note that the assumption regarding is of crucial importance. More specifically, Phillips et al. (2013a) showed that the shape of the asymptotic distribution of the test statistic depends heavily on the specification of .
[9] This point is made more formally by Phillips et al. (2015).
[10] For instance, one might wish to impose a minimal condition on the duration of the bubble component. To avoid false positive detection, the bubble’s duration should exceed a certain period, e.g. one year. If this is the case, supposing the sample size, T, is 30 years (360 months), is set equal to 0.7 for yearly data and to 5 for monthly data. Mathematically, for yearly data:
BIBLIOGRAPHY
Bariviera, A. F. (2017). “The Inefficiency of Bitcoin revisited: A dynamic approach”. Economics Letters, 161: 1–4.
Blanchard, O.J. (1979). “Speculative Bubbles, Crashes and Rational Expectations”. Economics Letters, 3(4): 387–389.
Blanchard, O.J. & Watson, M.W. (1982). “Bubbles, Rational Expectations and Financial Markets”. National Bureau of Economic Research, Working Paper, n. 945.
Campbell, J. Y., Lo, A.W. & MacKinlay, A.C. (1997). “The Econometrics of Financial Markets”. Princeton University Press, Princeton.
Campbell, J.Y. & Shiller, R.J. (1988). “The dividend-price ratio and expectations of future dividends and discount factors”. Review of Financial Studies, 1(3): 195–228.
Diba, B.T. & Grossman, H.I. (1985). “Rational Bubbles in Stock Prices?”. National Bureau of Economic Research, Working Paper, n. 1779.
Diba, B.T. & Grossman, H.I. (1987). “On the Inception of Rational Bubbles”. Quarterly Journal of Economics, 8(7): 697–700.
Diba, B.T. & Grossman, H.I. (1988). “The Theory of Rational Bubbles in Stock Prices”. Economic Journal 98: 746–757.
Engel, C., & West, K. D., (2005). “Exchange Rates and Fundamentals”. The Journal of Political Economy 113: 485-517.
Evans, G.W. (1991). “Pitfalls in testing for explosive bubbles in asset prices”. American Economic Review, 81: 922–930.
Phillips, P.C.B., & Magdalinos, T. (2007a). “Limit theory for Moderate Deviations from a Unit Root”. Journal of Econometrics, 136(1): 115–130.
Phillips, P.C.B. & Shi, S. (2017). “Financial Bubble Implosion and Reverse Regression”. International Economic Review, 34(4): 705–753.
Phillips, P.C.B., Shi, S., & Yu, J. (2013a). “Specification Sensitivity in Right-Tailed Unit Root Testing for Explosive Behaviour”. Oxford Bulletin of Economics and Statistics, 76(3): 315–333.
Phillips, P.C.B., Shi, S., & Yu, J. (2015a). “Testing for Multiple Bubbles: Historical Episodes of Exuberance and Collapse in the S&P500”. International Economic Review, 56(4): 1043–1078.
Phillips, P.C.B., Shi, S. & Yu, J. (2015b). “Testing for Multiple Bubbles: Limit Theory of Real-Time Detectors”. International Economic Review, 56 (4): 1079–1134.
Phillips, P.C.B., Wu, Y. & Yu, J. (2011). “Explosive Behaviour in the 1990s NASDAQ: When did exuberance escalate asset values?” International Economic Review, 52(1): 201–226.
Roubini, N. (2018). “Exploring the Cryptocurrency and Blockchain Ecosystem”. Testimony for the Hearing of the US Senate Committee on Banking, Housing and Community Affairs.
Sarno, L., & Taylor, M. P. (2002). “The Economics of Exchange Rates”. Cambridge University Press.
Sornette, D., Cauwels, P., Smilyanov, G. (2018). “Can we use volatility to diagnose financial bubbles? Lessons from 40 historical bubbles”. Quantitative Finance and Economics, 2(1): 486–594.
Weber, B. (2014). “Can Bitcoin Compete with Money?”. The Journal of Peer Production, 4: 6 pages.
Yermack, D. (2013). “Is Bitcoin a Real Currency? An economic appraisal”. Working Paper.
Pavlidis, G., E., Paya, I., & Peel, D., A. (2017). “Testing for speculative Bubbles Using Spot and Forward Prices”. International Economic Review, 58(4): 1191–1226.



![{\displaystyle P_{t}={\tfrac {1}{1+R}}E_{t}(P_{t+1}+D_{t+1}),t>0\qquad [1.1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d9102af969142fbd10e2edb86989681e55ee035)
![{\displaystyle P_{t}=\sum _{i=1}^{\infty }({\tfrac {1}{1+R}})^{i}E_{t}(D_{t+1})+\lim _{i\to \infty }({\tfrac {1}{1+R}})^{i}E_{t}(P_{t+1})\qquad [1.2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d08c64bbb8c8da64aaf8c5773e2f2f4e374037ef)

![{\displaystyle {\begin{aligned}P_{t}=P_{t}^{f}+B_{t},\\s.t.<math>E_{t}(B_{t+1})=(1+R)B_{t}\end{aligned}}\qquad [1.3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7df7848ae252d2686b96156dd1afc4c990cacf9)




![{\displaystyle B_{t+1}=\left\{{\begin{array}{cl}{\frac {(1+r)}{\pi }}B_{t}+\varepsilon _{t+1}&,{\text{ with probability }}\pi \\\varepsilon _{t+1}&,{\text{ with probability }}1-\pi \end{array}}\right.\qquad [2.1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/322285ccd3c516e119bd7ca0f7c68f0fe29b54a2)




![{\displaystyle B_{t+1}={\begin{cases}\psi B_{t}u_{t+1}&{\text{, if }}B_{t}\leq \tau \\{\left[k+{\frac {\psi }{\pi }}\left(B_{t}-{\frac {k}{\psi }}\right)v_{t}\right]u_{t+1}}&{\text{, if }}B_{t}>\tau \end{cases}}\qquad [2.2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a6f1a7571520fa6bde53764419fd094932ec86d)







![{\displaystyle y_{t}=dT^{-\eta }+\delta y_{t-1}+\varepsilon _{t},\varepsilon _{t}\thicksim IID(0,\sigma ^{2}),\delta =1\qquad [2.3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/150f9c3052af36966a7ee64dd7ee8facec722c49)



![{\displaystyle y_{t}=\mu +\delta y_{t-1}+\sum _{i=1}^{p}\psi _{i}\Delta y_{t-1}+\varepsilon _{t},\quad \varepsilon _{t}\backsim IID(0,\sigma ^{2})\qquad [2.4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7afaf70df39a51206417c64988379709dd9193c1)





![{\displaystyle y_{t}=\mu _{r_{1},r_{2}}+\delta _{r_{1},r_{2}}y_{t-1}+\sum _{i=1}^{p}\psi _{r_{1},r_{2}}^{i}\Delta y{t-1}+\varepsilon _{t},\quad \varepsilon _{t}\backsim IID(0,\sigma _{r_{1},r_{2}}^{2})\qquad [2.5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a89c7ac1a110a59296671dbd589292be75fbbc47)









![{\displaystyle GSADF\left(r_{0}\right)=\sup _{\underset {\left.r_{2}\in [r_{0};\ 1\right]}{r_{1}\in \left[0;\ r_{2}-r_{0}\right]}}\left\{ADF_{r_{1}}^{r_{2}}\right\}\qquad [2.6]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a17757656c18d1d57c72f75448d7d19b41769f97)
![{\displaystyle GSADF\left(r_{0}\right){\stackrel {d}{\rightarrow }}\sup _{\underset {r_{2}\in \left[r_{0};\ 1\right]}{r_{1}\in \left[0;\ r_{2}-r_{0}\right]}}\left\{{\frac {{\frac {1}{2}}r_{w}\left[W\left(r_{2}\right)^{2}-W\left(r_{1}\right)^{2}-r_{w}\right]-\int _{r_{1}}^{r_{2}}W(r)dr\left[W\left(r_{2}\right)-W\left(r_{1}\right)\right]}{r_{w}^{1/2}\left\{r_{w}\int _{r_{1}}^{r_{2}}W(r)^{2}dr-\left[\int _{r_{1}}^{r_{2}}W(r)dr\right]^{2}\right\}^{1/2}}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed3180d2ce7f4be2b99475b9466f237946fad2d9)


![{\displaystyle \operatorname {BSADF} {r_{2}}\left(r_{0}\right)=\sup _{r_{1}\in \left[0;r_{2}-r_{0}\right]}\left\{BADF{r_{1}}^{r_{2}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bd25b400994731bf53fa79c8f7a21d33e8a2c10)








![{\displaystyle {\widehat {r}}e=\inf _{r_{2}\in \left[r_{0};1\right]}\left\{r_{2}:BSADF_{r_{2}}\left(r_{0}\right)>scv_{r_{2}}^{\beta _{T}}\right\}\qquad [2.7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a44f7d626752d75b19b95657213565d2f8b749e0)
![{\displaystyle {\hat {r}}_{f}=\inf {r_{2}\in \left[{\widehat {r}}_{e}+\delta \log(T)/T;1\right]}\left\{r_{2}:BSADF{r_{2}}\left(r_{0}\right)<\operatorname {scv} _{r_{2}}^{\beta _{T}}\right\}\qquad [2.8]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfe71685664ed45f014177996695cdbec06525fe)





![{\displaystyle \operatorname {GSADF} \left(r_{0}\right)=\sup {r_{2}\in \left[r_{0};1\right]}\left\{BSADF{r2}\left(r_{0}\right)\right\}\qquad [2.9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/993fd26a91fa05ddce0369d4599c92ec00949951)

![{\displaystyle s_{t}=v_{t}+B_{t}\qquad [2.10]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73954bf74710622fb1eb7650efd43d842af479d3)
![{\displaystyle v_{t}=\phi v_{t-1}+\theta _{t}\qquad [2.11]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f0800b729bd10fe9e11bd9b60db18250a0dbfde)

![{\displaystyle f_{t,n}=E_{t}\left[s_{t+n}\right]=E_{t}\left[v_{t+n}\right]+E_{t}\left[B_{t+n}\right]\qquad [2.12]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a5c3a405aeb93c9bcbd27fb68c1297224c7a086)
![{\displaystyle f_{t,n}=\phi ^{n}v_{t}+(1+r)^{n}B_{t}\qquad [2.13]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/429281f14457716af3160b655b50c722daff0d53)
![{\displaystyle s_{t+n}=v_{t+n}+B_{t+n}\qquad [2.14]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65dd7ffe689a8a6a286539fd5b67a4201af8b6cf)
![{\displaystyle s_{t+n}=\phi ^{n}v_{t}+\left({\frac {1+r}{\pi }}\right)^{n}B_{t}+\varepsilon _{t+n}^{*}\qquad [2.15]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0173b0c23a8f2204bcb5fc9249523ec00b11398b)












![{\displaystyle E_{t}\left[E_{t+1}[X]\right]=E_{t}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2d9a8c878bc39b401dc52cdb76c875a3b1227bb)